خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
ترسیم نمودار معادلات درجه دوم در شکل استاندارد

یک تابع درجه دوم تابعی در شکل زیر می باشد. در این آموزش معانی ثابت های a، b، و c در یک معادلۀ درجه دوم در شکل استاندارد را متوجه می شوید. همچنین با کمک معادلۀ یک تابع درجه دوم در شکل استاندارد آن، نمودارش را ترسیم می کنید.

یک تابع درجه دوم در شکل \(f(x)=ax^2+bx+c\) در شکل استاندارد می باشد. صرفنظر از اندازۀ شکل، نمودار یک تابع درجه دوم سهمی (شلجمی) نام دارد.
هر ضریب در یک تابع درجه دوم در شکل استاندارد، تاثیری بر روی شکل و محل قرار گیری نمودار آن تابع دارد.
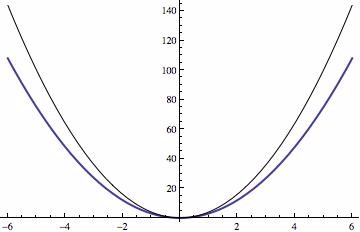
ضریب \(a\) سرعت کاهش یا افزایش یک تابع درجه دوم از رأس آن را نشان می دهد. یک مقدار مثبت بزرگتر از \(a\) منجر می شود تا تابع مربوطه سریعتر افزایش یابد و نمودارش نازکتر باشد. در تصویر زیر منحنی سیاه رنگ نمودار تابع \(y=4x^2\) می باشد، در حالیکه منحنی آبی رنگ نمودار تابع \(y=3x^2\) می باشد. منحنی سیاه رنگ نازکتر به نظر می آید و دلیلش هم اینست که ضریب \(a\) آن از منحنی آبی رنگ بزرگتر است.
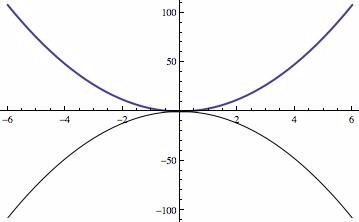
همچنین جهت باز شدن سهمی رو به بالا یا پایین نیز توسط ضریب \(a\) کنترل می شود. اگر ضریب \(a \gt 0\) باشد، سهمی رو به بالا باز می شود، و اگر ضریب \(a \lt 0\) باشد، سهمی رو به پایین باز می شود. در تصویر زیر سهمی آبی رنگ، نمودار تابع \(y=3x^2\) است. از آنجا که \(a=3 \gt 0\) است، این سهمی رو به بالا باز شده است. سهمی سیاه رنگ، نمودار تابع \(y=-3x^2\) است. از آنجا که \(a=-3 \lt 0\) است، این سهمی رو به پایین باز شده است.
ضرایب \(b\) و \(a\)، همراه با یکدیگر، محور تقارن یک سهمی، و مختصات \(x\) رأس آن را کنترل می کنند. محور تقارن در یک سهمی با فرمول زیر بدست می آید.
$$x=-\frac{b}{2a}$$
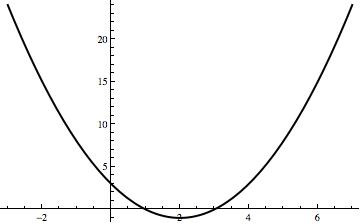
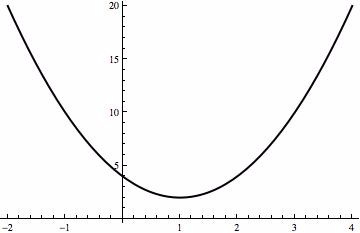
به عنوان مثال، سهمی \(y=2x^2-4x+4\) را که در تصویر زیر نشان داده شده است، در نظر بگیرید. از آنجا که \(a=2\) و \(b=-4\) است، محور تقارن آن اینست:
$$x=-\frac{-4}{2 \cdot 2}=1$$
در نتیجه مشخص می شود که مختصات \(x\) رأس این نمودار \(1\) است.
ضریب \(c\) ارتقاع سهمی را کنترل می کند. اگر دقیق تر بگوییم، \(c\) نقطه ای است که سهمی محور \(y\) را قطع می کند. نقطۀ \((0,c)\) عرض از مبدأ سهمی می باشد. در مثال بالا توجه کنید که \(c=4\) است و در نقطۀ \((0,4)\) محور \(y\) را قطع می کند.

تابع درجه دوم در شکل استاندارد (Standard Form):
$$y=ax^2+bx+c$$نکات کلیدی
-
نمودار یک تابع درجه دوم (quadratic function) یک سهمی (parabola) می باشد که محور تقارن آن با محور \(y\) موازی می باشد.
-
ضریب های \(a\)، \(b\)، و \(c\) در معادلۀ \(y=ax^2+bx+c\) جنبه های مختلف این سهمی را کنترل می کنند.
اصطلاحات کلیدی
-
رأس (vertex): بیشترین یا کمترین مقدار یک تابع درجه دوم.
-
سهمی (parabola): شکلی که توسط نمودار یک تابع درجه دوم ساخته می شود.
-
درجه دوم (quadratic): یک چندجمله ای با درجۀ دو.
سهمی
یک تابع درجه دوم در شکل \(f(x)=ax^2+bx+c\) در شکل استاندارد می باشد. صرفنظر از اندازۀ شکل، نمودار یک تابع درجه دوم سهمی (شلجمی) نام دارد.
ضرایب (Coefficients) و نمودار یک تابع درجه دوم
هر ضریب در یک تابع درجه دوم در شکل استاندارد، تاثیری بر روی شکل و محل قرار گیری نمودار آن تابع دارد.
ضریب \(x^2\) یعنی \(a\)
ضریب \(a\) سرعت کاهش یا افزایش یک تابع درجه دوم از رأس آن را نشان می دهد. یک مقدار مثبت بزرگتر از \(a\) منجر می شود تا تابع مربوطه سریعتر افزایش یابد و نمودارش نازکتر باشد. در تصویر زیر منحنی سیاه رنگ نمودار تابع \(y=4x^2\) می باشد، در حالیکه منحنی آبی رنگ نمودار تابع \(y=3x^2\) می باشد. منحنی سیاه رنگ نازکتر به نظر می آید و دلیلش هم اینست که ضریب \(a\) آن از منحنی آبی رنگ بزرگتر است.
همچنین جهت باز شدن سهمی رو به بالا یا پایین نیز توسط ضریب \(a\) کنترل می شود. اگر ضریب \(a \gt 0\) باشد، سهمی رو به بالا باز می شود، و اگر ضریب \(a \lt 0\) باشد، سهمی رو به پایین باز می شود. در تصویر زیر سهمی آبی رنگ، نمودار تابع \(y=3x^2\) است. از آنجا که \(a=3 \gt 0\) است، این سهمی رو به بالا باز شده است. سهمی سیاه رنگ، نمودار تابع \(y=-3x^2\) است. از آنجا که \(a=-3 \lt 0\) است، این سهمی رو به پایین باز شده است.
محور تقارن (The Axis of Symmetry)
ضرایب \(b\) و \(a\)، همراه با یکدیگر، محور تقارن یک سهمی، و مختصات \(x\) رأس آن را کنترل می کنند. محور تقارن در یک سهمی با فرمول زیر بدست می آید.
$$x=-\frac{b}{2a}$$
به عنوان مثال، سهمی \(y=2x^2-4x+4\) را که در تصویر زیر نشان داده شده است، در نظر بگیرید. از آنجا که \(a=2\) و \(b=-4\) است، محور تقارن آن اینست:
$$x=-\frac{-4}{2 \cdot 2}=1$$
در نتیجه مشخص می شود که مختصات \(x\) رأس این نمودار \(1\) است.
عرض از مبدأ (y-intercept) در یک سهمی
ضریب \(c\) ارتقاع سهمی را کنترل می کند. اگر دقیق تر بگوییم، \(c\) نقطه ای است که سهمی محور \(y\) را قطع می کند. نقطۀ \((0,c)\) عرض از مبدأ سهمی می باشد. در مثال بالا توجه کنید که \(c=4\) است و در نقطۀ \((0,4)\) محور \(y\) را قطع می کند.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: