خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 13: قانون کسینوس، استفادۀ کاربردی

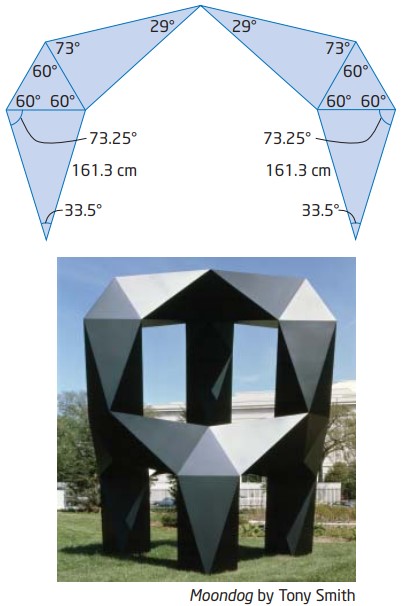
تونی اسمیت (Tony Smith) در سال \(1912\) در "اورنج جنوبی" (South Orange) در نیوجرسی بدنیا آمد. در کودکی او از بیماری سل (tuberculosis) رنج می برد. او زمانش را صرف بازی کردن با جعبه های داروها می کرد. یکی از مجسمه های ساخت او با نام "مونداگ" (Moondog) متشکل از چندین مثلث متساوی الاضلاع و متساوی الساقین می باشد که هنر و ریاضیات را با یکدیگر ترکیب کرده اند. از اطلاعات ارائه شده در طرح زیر برای تعیین ماکزیمم عرض مونداگ استفاده کنید.


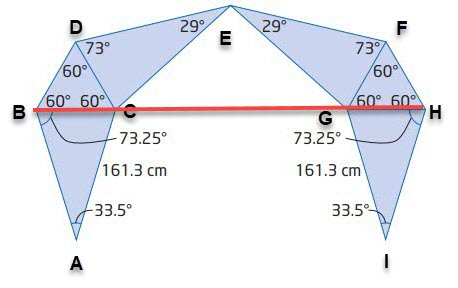
چیزی که بدنبالش هستیم \(BH\) یعنی خط قرمزی است که در تصویر زیر می بینید، می باشد.
$$
BH = BC + CG + GH
$$
برای رسیدن به این مقادیر روی سه تا از مثلث ها از قوانین سینوس و کسینوس استفاده می کنیم. دقت کنید که مثلث های روبروی آنها هم شکل و هم اندازه هستند و در نتیجه مقادیر بدست آمده در این سه مثلث عیناً در سه مثلث روبرویی نیز تکرار می شود، هرچند می توانید این هم اندازه و هم شکل بودن را نیز نادیده بگیرید و روی هر شش مثلث عملیات مربوطه را انجام دهید.
ابتدا از \(\triangle{ABC}\) آغاز می کنیم:
$$
\text{In } \triangle{ABC} \text{:}\\
\frac{a}{\sin A} = \frac{b}{\sin B}\\
\frac{a}{\sin 33.5^{\circ}} = \frac{161.3}{\sin 73.25^{\circ}}\\
a = \frac{161.3 \sin 33.5^{\circ}}{\sin 73.25^{\circ}} = 92.972...\\
a = BC \approx 93.0 \text{ cm}
$$
سپس به سراغ \(\triangle{DBC}\) می رویم، از آنجا که این مثلث یک مثلث متساوی الاضلاع می باشد همۀ اضلاع آن با هم برابر خواهند بود:
$$
\text{In } \triangle{DBC} \text{:}\\
d=b=c=93.0 \text{ cm}
$$
حال به سراغ \(\triangle{DCE}\) می رویم:
$$
\text{In } \triangle{DCE} \text{:}\\
\angle{C} = 180^{\circ} - 73^{\circ} - 29^{\circ} = 78^{\circ}\\
\text{ }\\[2ex]
\frac{d}{\sin D} = \frac{e}{\sin E}\\
\frac{d}{\sin 73^{\circ}} = \frac{93.0}{\sin 29^{\circ}}\\
d = \frac{93 \sin 73^{\circ}}{\sin 29^{\circ}} = 183.445...\\
d = CE \approx 183.4 \text{ cm}
$$
تکۀ بعدی پازل ما در \(\triangle{CEG}\) می باشد:
$$
\text{In } \triangle{CEG} \text{:}\\
\angle{C} = \angle{BCG} - \angle{BCD} - \angle{DCE} \\
\angle{C} = 180^{\circ} - 60^{\circ} - 78^{\circ} = 42^{\circ}\\
\angle{G} = \angle{C} = 42^{\circ}\\
\angle{E} = 180^{\circ} - 42^{\circ} - 42^{\circ} = 96^{\circ} \\
\text{ }\\[2ex]
\frac{e}{\sin E} = \frac{c}{\sin C}\\
\frac{e}{\sin 96^{\circ}} = \frac{183.4}{\sin 42^{\circ}}\\
e = \frac{183.4 \sin 96^{\circ}}{\sin 42^{\circ}} = 272.585...\\
e = CG \approx 272.6 \text{ cm}
$$
هم اکنون همۀ پارامترهای لازم برای رسیدن به پاسخ نهایی را در اختیار داریم:
$$
BH = BC + CG + GH\\
BH = 93.0 + 272.6 + 93.0 = 458.6 \text{ cm}
$$


پاسخ

چیزی که بدنبالش هستیم \(BH\) یعنی خط قرمزی است که در تصویر زیر می بینید، می باشد.

$$
BH = BC + CG + GH
$$
برای رسیدن به این مقادیر روی سه تا از مثلث ها از قوانین سینوس و کسینوس استفاده می کنیم. دقت کنید که مثلث های روبروی آنها هم شکل و هم اندازه هستند و در نتیجه مقادیر بدست آمده در این سه مثلث عیناً در سه مثلث روبرویی نیز تکرار می شود، هرچند می توانید این هم اندازه و هم شکل بودن را نیز نادیده بگیرید و روی هر شش مثلث عملیات مربوطه را انجام دهید.
ابتدا از \(\triangle{ABC}\) آغاز می کنیم:
$$
\text{In } \triangle{ABC} \text{:}\\
\frac{a}{\sin A} = \frac{b}{\sin B}\\
\frac{a}{\sin 33.5^{\circ}} = \frac{161.3}{\sin 73.25^{\circ}}\\
a = \frac{161.3 \sin 33.5^{\circ}}{\sin 73.25^{\circ}} = 92.972...\\
a = BC \approx 93.0 \text{ cm}
$$
سپس به سراغ \(\triangle{DBC}\) می رویم، از آنجا که این مثلث یک مثلث متساوی الاضلاع می باشد همۀ اضلاع آن با هم برابر خواهند بود:
$$
\text{In } \triangle{DBC} \text{:}\\
d=b=c=93.0 \text{ cm}
$$
حال به سراغ \(\triangle{DCE}\) می رویم:
$$
\text{In } \triangle{DCE} \text{:}\\
\angle{C} = 180^{\circ} - 73^{\circ} - 29^{\circ} = 78^{\circ}\\
\text{ }\\[2ex]
\frac{d}{\sin D} = \frac{e}{\sin E}\\
\frac{d}{\sin 73^{\circ}} = \frac{93.0}{\sin 29^{\circ}}\\
d = \frac{93 \sin 73^{\circ}}{\sin 29^{\circ}} = 183.445...\\
d = CE \approx 183.4 \text{ cm}
$$
تکۀ بعدی پازل ما در \(\triangle{CEG}\) می باشد:
$$
\text{In } \triangle{CEG} \text{:}\\
\angle{C} = \angle{BCG} - \angle{BCD} - \angle{DCE} \\
\angle{C} = 180^{\circ} - 60^{\circ} - 78^{\circ} = 42^{\circ}\\
\angle{G} = \angle{C} = 42^{\circ}\\
\angle{E} = 180^{\circ} - 42^{\circ} - 42^{\circ} = 96^{\circ} \\
\text{ }\\[2ex]
\frac{e}{\sin E} = \frac{c}{\sin C}\\
\frac{e}{\sin 96^{\circ}} = \frac{183.4}{\sin 42^{\circ}}\\
e = \frac{183.4 \sin 96^{\circ}}{\sin 42^{\circ}} = 272.585...\\
e = CG \approx 272.6 \text{ cm}
$$
هم اکنون همۀ پارامترهای لازم برای رسیدن به پاسخ نهایی را در اختیار داریم:
$$
BH = BC + CG + GH\\
BH = 93.0 + 272.6 + 93.0 = 458.6 \text{ cm}
$$
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: