خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
تمرین 3: نامساوی های خطی با دو متغیر، تمرین

نامساوی های زیر را در نظر بگیرید.

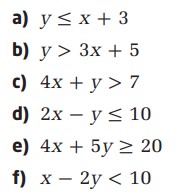
برای تعیین شیب خط و همچنین عرض از مبدأ، ابتدا معادلۀ خط مرتبط با نامساوی را در شکل شیب-تقاطع، \(y = mx + b\)، می نویسیم. در این شکل ضریب \(x\) یعنی \(m\) برابر با شیب و \(b\) برابر با عرض از مبدأ می باشد. برای تعیین توپر یا خط چین بودن کرانه، به علامت نامساوی توجه می کنیم، اگر علامت نامساوی \(\lt\) یا \(\gt\) باشد، کرانه خط چین می باشد. اگر علامت نامساوی \(\le\) یا \(\ge\) باشد، کرانه خط توپر می باشد.

-
اگر ضرورت داشته باشد، \(y\) را با جملات \(x\) بیان کنید. شیب خط و عرض از مبدأ را تعیین کنید.
-
تعیین کنید که آیا کرانه یک خط توپر یا یک خط چین است.
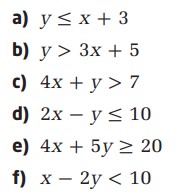
پاسخ
برای تعیین شیب خط و همچنین عرض از مبدأ، ابتدا معادلۀ خط مرتبط با نامساوی را در شکل شیب-تقاطع، \(y = mx + b\)، می نویسیم. در این شکل ضریب \(x\) یعنی \(m\) برابر با شیب و \(b\) برابر با عرض از مبدأ می باشد. برای تعیین توپر یا خط چین بودن کرانه، به علامت نامساوی توجه می کنیم، اگر علامت نامساوی \(\lt\) یا \(\gt\) باشد، کرانه خط چین می باشد. اگر علامت نامساوی \(\le\) یا \(\ge\) باشد، کرانه خط توپر می باشد.
-
نامساوی: \(y \le x + 3\)
خط مرتبط: \(y = x+ 3\)
شیب خط: \(1\)
عرض از مبدأ: \(3\)
شکل کرانه: خط توپر
-
نامساوی: \(y \gt 3x + 5\)
خط مرتبط: \(y = 3x + 5\)
شیب خط: \(3\)
عرض از مبدأ: \(5\)
شکل کرانه: خط چین
-
نامساوی: \(y \gt -4x + 7\)
خط مرتبط: \(y = -4x + 7\)
شیب خط: \(-4\)
عرض از مبدأ: 7
شکل کرانه: خط چین
-
نامساوی: \(y \ge 2x -10\)
خط مرتبط: \(y = 2x - 10\)
شیب خط: \(2\)
عرض از مبدأ: \(-10\)
شکل کرانه: خط توپر
-
نامساوی: \(y \ge -\frac{4}{5}x + 5\)
خط مرتبط: \(y = -\frac{4}{5}x + 4\)
شیب خط: \(-\frac{4}{5}\)
عرض از مبدأ: \(4\)
شکل کرانه: خط توپر
-
نامساوی: \(y \gt \frac{1}{2}x -5\)
خط مرتبط: \(y=\frac{1}{2}x -5\)
شیب خط: \(\frac{1}{2}\)
عرض از مبدأ: \(-5\)
شکل کرانه: خط چین
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: