خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
مکعب مستطیل و مکعب مربع

در این آموزش با مکعب مستطیل و مکعب مربع آشنا می شویم. همچنین با مفاهیمی همچون مساحت رویۀ مکعب مستطیل، حجم مکعب مستطیل، قطر مکعب و تفاوت آن با قطر وجه مکعب، و چگونگی یافتن قطر یک مکعب آشنا می شویم.

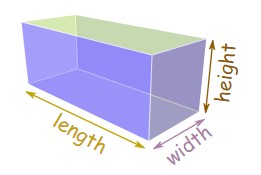
مکعب مستطیل شکلی شبیه یک جعبه است. دارای شش وجه مسطح می باشد و تمامی زوایای آن زاویۀ قائمه می باشند. و تمامی وجه های آن مستطیل می باشند. همچنین مکعب مستطیل یک منشور (prism) نیز می باشد زیرا در امتداد طول آن دارای سطح مقطع (cross-section) یکسانی می باشد. در واقع یک منشور مکعبی (rectangular prism) است.
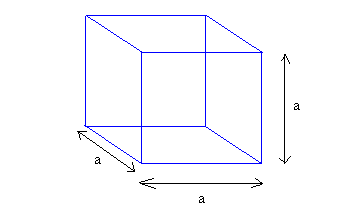
هنگامی که هر سه طول یک مکعب مستطیل با یکدیگر برابر باشند، آن را مکعب مربع می نامیم و در این حالت تمامی وجه های آن مربع می باشند. یک مکعب مربع هنوز هم یک منشور است. در واقع مکعب مربع نوع خاصی از مکعب مستطیل است و قوانین مکعب مستطیل بر روی آن نیز صادقند.
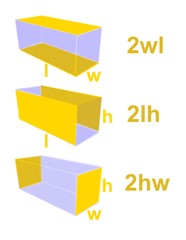
مساحت رویه از فرمول زیر بدست می آید:
\(\text{Area = 2 × Width × Length + 2 × Length × Height + 2 × Width × Height}\)
که به طور خلاصه می توانیم آن را اینگونه بنویسیم:
\(\text{A = 2wl + 2lh + 2hw}\)
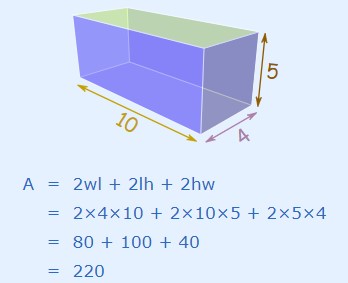
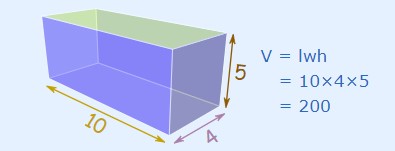
به مثال زیر توجه کنید:
حجم یک مکعب مستطیل از فرمول زیر بدست می آید:
\(\text{Volume = Length × Width × Height}\)
که به طور خلاصه آن را اینکه می نویسیم:
\(\text{V = l × w × h}\)
و حتی می توانیم خلاصه ترش هم بکنیم:
\(\text{V = lwh}\)
به مثال زیر توجه کنید:
به تصویر زیر دقت کنید:
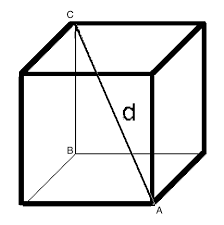
خط \(d\) دو رأس \(\text{A}\) و \(\text{B}\) را به یکدیگر متصل می کنند. این خط قطر مکعب می باشد. یعنی دو گوشۀ روبرو را به یکدیگر متصل می کنند. حالا به تصویر بعدی نگاه کنید:
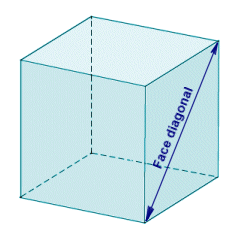
آنچه که در تصویر بالا دیدید، قطر یک وجه از مکعب می باشد.
نکته: برای محاسبۀ قطر یک مکعب نیاز به قطر وجه آن نیز داریم و برای همین مهم است که هر دو مفهوم را خوب درک کنید.
برای درک این موضوع همراه با یک مثال آن را توضیح می دهیم.
طول قطر یک مکعب مربع را که طول ضلع آن \(4 \text{ CM}\) است، بیابید:
کار را با یک تصویر آغاز می کنیم، توجه کنید که قطر مکعب در تصویر زیر با \(x\) نامگذاری شده است، طول قطر برابر با فاصلۀ یک گوشه از این مکعب تا گوشۀ مقابل آن از این سو به آن سوی مکعب می باشد.
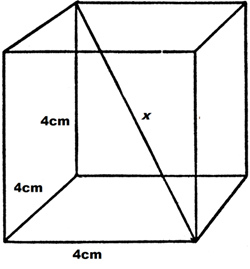
ترفند حل این مسأله اینست که قطر وجه پایینی این مکعب را نیز ترسیم کنیم، که در تصویر زیر آن را \(y\) نامگذاری کرده ایم. در واقع قطر وجه، قطر یکی از وجه های این مکعب می باشد که در اینجا وجه پایینی آن را در نظر گرفته ایم.
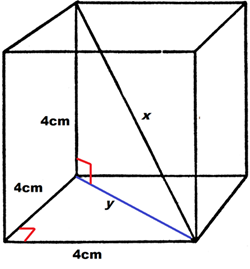
توجه کنید که این کار دو مثلث قائم الزاویه می سازد. اگرچه هدف نهایی ما یافتن \(x\) است، اما می توانیم با یافتن \(y\) کار را شروع کنیم. با استفاده از قضیۀ فیثاغورث و با توجه به اینکه دو ساق مثلث قائم الزاویۀ پایین را داریم به سادگی \(y\) را می یابیم. در واقع \(y\) وتر مثلث قائم الزاویۀ پایینی است و در عین حال یکی از ساق های مثلث قائم الزاویۀ بالایی نیز می باشد.
$$4^2 + 4^2 = y^2 \\
16 + 16 = y^2 \\
32 = y^2 \\
\sqrt{32} = y \\
\sqrt{16 \cdot 2} = y\\
\sqrt{16} \cdot \sqrt{2} = y\\
4\sqrt{2} = y$$
حالا که مقدار \(y\) را می دانیم، می توانیم دوباره از قضیۀ فیثاغورث، این بار بر روی مثلث قائم الزاویۀ بالایی، استفاده کنیم:
$$4^2 + \biggl( 4\sqrt{2} \biggr)^2 = x^2 \\
16 + 32 = x^2 \\
48 = x^2 \\
\sqrt{48} = x \\
4\sqrt{3} = x$$
همانطور که دیدید طول قطر این مکعب برابر با \(4\sqrt{3} \text{ CM}\) می باشد.

مکعب مستطیل (cuboid)
مکعب مستطیل شکلی شبیه یک جعبه است. دارای شش وجه مسطح می باشد و تمامی زوایای آن زاویۀ قائمه می باشند. و تمامی وجه های آن مستطیل می باشند. همچنین مکعب مستطیل یک منشور (prism) نیز می باشد زیرا در امتداد طول آن دارای سطح مقطع (cross-section) یکسانی می باشد. در واقع یک منشور مکعبی (rectangular prism) است.

مکعب مربع (Cube)
هنگامی که هر سه طول یک مکعب مستطیل با یکدیگر برابر باشند، آن را مکعب مربع می نامیم و در این حالت تمامی وجه های آن مربع می باشند. یک مکعب مربع هنوز هم یک منشور است. در واقع مکعب مربع نوع خاصی از مکعب مستطیل است و قوانین مکعب مستطیل بر روی آن نیز صادقند.

مساحت رویۀ مکعب مستطیل (Surface Area)
مساحت رویه از فرمول زیر بدست می آید:
\(\text{Area = 2 × Width × Length + 2 × Length × Height + 2 × Width × Height}\)
که به طور خلاصه می توانیم آن را اینگونه بنویسیم:
\(\text{A = 2wl + 2lh + 2hw}\)

به مثال زیر توجه کنید:

حجم مکعب مستطیل (Volume)
حجم یک مکعب مستطیل از فرمول زیر بدست می آید:
\(\text{Volume = Length × Width × Height}\)
که به طور خلاصه آن را اینکه می نویسیم:
\(\text{V = l × w × h}\)
و حتی می توانیم خلاصه ترش هم بکنیم:
\(\text{V = lwh}\)
به مثال زیر توجه کنید:

قطر مکعب (diagonal)
به تصویر زیر دقت کنید:

خط \(d\) دو رأس \(\text{A}\) و \(\text{B}\) را به یکدیگر متصل می کنند. این خط قطر مکعب می باشد. یعنی دو گوشۀ روبرو را به یکدیگر متصل می کنند. حالا به تصویر بعدی نگاه کنید:

آنچه که در تصویر بالا دیدید، قطر یک وجه از مکعب می باشد.
نکته: برای محاسبۀ قطر یک مکعب نیاز به قطر وجه آن نیز داریم و برای همین مهم است که هر دو مفهوم را خوب درک کنید.
چگونه قطر یک مکعب را بیابیم؟
برای درک این موضوع همراه با یک مثال آن را توضیح می دهیم.
طول قطر یک مکعب مربع را که طول ضلع آن \(4 \text{ CM}\) است، بیابید:
کار را با یک تصویر آغاز می کنیم، توجه کنید که قطر مکعب در تصویر زیر با \(x\) نامگذاری شده است، طول قطر برابر با فاصلۀ یک گوشه از این مکعب تا گوشۀ مقابل آن از این سو به آن سوی مکعب می باشد.

ترفند حل این مسأله اینست که قطر وجه پایینی این مکعب را نیز ترسیم کنیم، که در تصویر زیر آن را \(y\) نامگذاری کرده ایم. در واقع قطر وجه، قطر یکی از وجه های این مکعب می باشد که در اینجا وجه پایینی آن را در نظر گرفته ایم.

توجه کنید که این کار دو مثلث قائم الزاویه می سازد. اگرچه هدف نهایی ما یافتن \(x\) است، اما می توانیم با یافتن \(y\) کار را شروع کنیم. با استفاده از قضیۀ فیثاغورث و با توجه به اینکه دو ساق مثلث قائم الزاویۀ پایین را داریم به سادگی \(y\) را می یابیم. در واقع \(y\) وتر مثلث قائم الزاویۀ پایینی است و در عین حال یکی از ساق های مثلث قائم الزاویۀ بالایی نیز می باشد.
$$4^2 + 4^2 = y^2 \\
16 + 16 = y^2 \\
32 = y^2 \\
\sqrt{32} = y \\
\sqrt{16 \cdot 2} = y\\
\sqrt{16} \cdot \sqrt{2} = y\\
4\sqrt{2} = y$$
حالا که مقدار \(y\) را می دانیم، می توانیم دوباره از قضیۀ فیثاغورث، این بار بر روی مثلث قائم الزاویۀ بالایی، استفاده کنیم:
$$4^2 + \biggl( 4\sqrt{2} \biggr)^2 = x^2 \\
16 + 32 = x^2 \\
48 = x^2 \\
\sqrt{48} = x \\
4\sqrt{3} = x$$
همانطور که دیدید طول قطر این مکعب برابر با \(4\sqrt{3} \text{ CM}\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: