خوش آموز درخت تو گر بار دانش بگیرد، به زیر آوری چرخ نیلوفری را
توابع؛ دامنه و بُرد (Functions; Domain and Range)

توابع (Functions) اساس مطالعۀ حسابان (calculus) می باشند. در این فصل ما مرور می کنیم که توابع چه هستند و چگونه به شکل نمودارها (graphs) تصویر می شوند، چگونه ترکیب و تبدیل می شوند، و به چه روش هایی می توانند دسته بندی گردند. ما توابع مثلثاتی (trigonometric functions) را مرور می کنیم، و خطاهایی که می تواند در هنگام نمایش نمودار توابع توسط ماشین حسابها و کامپیوترها رُخ دهند را مورد بحث قرار می دهیم. همچنین توابع معکوس (inverse functions)، توابع نمایی (exponential functions)، توابع لگاریتمی (logarithmic functions) را مورد بحث قرار می دهیم. دستگاه اعداد حقیقی (real number system)، مختصات دکارتی (Cartesian coordinates)، خط های راست (straight lines)، دایره ها (circles)، سهمی ها (parabolas)، و بیضی ها (ellipses) در ضمائم مورد بررسی قرار می گیرند.

توابع ابزاری برای توصیف دنیای واقعی به لحاظ ریاضی می باشند. یک تابع می تواند با یک معادله (equation)، یک نمودار (graph)، یک جدول عددی (numerical table)، یا یک توصیف کلامی (verbal description) نمایش داده شود؛ ما در طول این کتاب از هر چهار نوع نمایش توابع استفاده خواهیم کرد. این بخش این مفاهیم توابع را مورد بررسی قرار می دهد.
دمایی که آب در آن به جوش می آید به ارتفاع از سطح دریا بستگی دارد (هرچقدر بالاتر بروید نقطۀ جوش سقوط می کند). بهرۀ پرداختی برای پول نقد سرمایه گذاری شده به طول مدتی که آن سرمایه نگهداشته شده است بستگی دارد. مساحت یک دایره به شعاع آن بستگی دارد. مسافت پیموده شده توسط یک شیء با سرعت ثابت در امتداد یک مسیر خط مستقیم، به زمان سپری شده بستگی دارد.
در هر مورد، مقدار کمیت یک متغیر، فرض کنید \(y\)، به مقدار کمیت متغیر دیگری بستگی دارد، که ممکن است آن را \(x\) بنامیم. ما می گوییم که \(y\) تابعی از \(x\) است (y is a function of x) و این را به صورت نمادین اینگونه می نویسیم:
$$y=f(x)$$
این را اینگونه می خوانیم: \(y\) برابر است با افِ ایکس (y equals ƒ of x)
در این نشانه گذاری، نماد \(f\) نشان دهندۀ تابع است، حرف \(x\) متغیر مستقل (independent variable) است که مقدار ورودی \(f\) را نشان می دهد، و \(y\) متغیر وابسته (dependent variable) یا مقدار خروجی \(f\) در \(x\) می باشد.
مجموعۀ \(D\) متشکل از تمامی مقادیر ورودی (input values) ممکن، دامنۀ (domain) این تابع نامیده می شود. مجموعۀ تمامی مقادیر خروجی (output values) از \(f(x)\) همینطور که \(x\) در سراسر \(D\) تغییر می کند، بُرد (range) این تابع نامیده می شود. این بُرد ممکن است شامل تمامی عناصر موجود در مجموعۀ \(Y\) نشود. دامنه و برد یک تابع می تواند هر مجموعه ای از اشیاء باشد، اما اغلب در حسابان آنها مجموعه ای از اعداد حقیقی (real numbers) می باشند که به نقاطی از یک خط مختصات تفسیر می گردند. (در فصل های \(\text{13-16}\)، با توابعی مواجه خواهیم شد که در آنها عناصر این مجموعه ها نقاطی در صفحۀ مختصات یا در فضا می باشند.)
اغلب یک تابع با یک فرمول معین می شود که چگونگی محاسبۀ مقدار خروجی از روی متغیر ورودی را توصیف می کند. به عنوان مثال، معادلۀ \(A=\pi r^2\) یک قاعده است که مساحت \(A\) یک دایره را از روی شعاع آن \(r\) محاسبه می کند (بنابراین، \(r\)، که به عنوان یک طول تفسیر می شود، در این فرمول فقط می تواند مثبت باشد). هنگامیکه یک تابع \(y=f(x)\) را با یک فرمول تعریف می کنیم و دامنۀ آن به صراحت بیان نمی شود یا با مفاد آن محدود نمی گردد، این دامنه به شکل بزرگترین مجموعه از مقادیر حقیقی \(x\) در نظر گرفته می شود که برای آنها این فرمول یک مقدار حقیقی \(y\) را نتیجه می دهد، به این دامنه، دامنۀ طبیعی (natural domain) گفته می شود. اگر می خواهیم این دامنه را به نحوی محدود کنیم، باید چنین بگوییم. دامنۀ \(y=x^2\) کل مجموعۀ اعداد حقیقی می باشد. فرض کنید می خواهیم دامنۀ این تابع را به مقادیر مثبت \(x\) محدود کنیم، آن را اینگونه می نویسیم:
$$y=x^2, x \gt 0$$
تغییر دادن دامنه ای که بر روی یک فرمول اِعمال می شود، معمولاً برد آن را نیز تغییر می دهد. بُرد \(y=x^2\) برابر با \([0,\infty)\) می باشد. برد \(y=x^2, x \ge 2\) برابر با مجموعۀ تمامی اعداد بدست آمده از مربع ساختن اعداد بزرگتر یا مساوی \(2\) می باشد. در نشانه گذاری مجموعه ها این برد به یکی از سه شکل زیر نوشته می شود:
$$\{x^2| x \ge 2\} \text{ or } \{ y|y \ge 4 \} \text{ or } [4,\infty)$$
هنگامیکه برد یک تابع مجموعه ای از اعداد حقیقی باشد، گفته می شود که آن تابع با مقدار حقیقی (real-valued) می باشد. دامنه ها و بردهای بیشتر توابع حقیقی (real-valued functions) از یک متغیر حقیقی که در نظر می گیریم، بازه ها (intervals) یا ترکیبی از بازه ها می باشند. بازه ها می توانند باز (open)، بسته (closed)، یا نیمه باز (half open) باشند، و می توانند متناهی (finite) یا نامتناهی (infinite) باشند. گاهی اوقات یافتن برد یک تابع آسان نمی باشد.
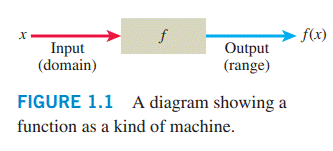
یک تابع \(f\) مانند دستگاهی است که هرگاه که یک مقدار ورودی \(x\) را از دامنه اش به آن وارد می کنیم یک مقدار خروجی \(f(x)\) را در بُردش تولید می کند (شکل \(\text{1.1}\)). دکمه های توابع بر روی یک ماشین حساب مثالی از یک تابع در شکل یک دستگاه می باشد. به عنوان مثال، دکمۀ \(\sqrt{x}\) بر روی یک ماشین حساب، هرگاه که شما یک عدد غیرمنفی را وارد کنید و این دکمه را بفشارید، یک مقدار خروجی (جذر) به شما می دهد.
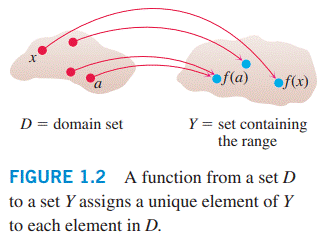
همچنین یک تابع می تواند به شکل یک نمودار فلش (arrow diagram) در نظر گرفته شود (شکل \(\text{1.2}\)). هر فلش یک عنصر از دامنۀ \(D\) را با یک عنصر یکتا یا واحد در مجموعۀ \(Y\) مرتبط می سازد. در شکل \(\text{1.2}\) فلش ها نشان می دهند که \(f(a)\) به \(a\) مرتبط است، \(f(x)\) به \(x\) مرتبط است، و به همین ترتیب. توجه داشته باشید که یک تابع می تواند به ازاء دو مقدار ورودی متفاوت از دامنۀ آن مقدار یکسانی را داشته باشد (همچنانکه در \(f(a)\) از شکل \(\text{1.2}\) رخ داده است)، اما هر عنصر ورودی \(x\) با یک مقدار خروجی واحد از \(f(x)\) مرتبط است.
مثال 1 بیایید دامنۀ طبیعی و بردهای مرتبط با آن را برای چند تابع ساده بررسی کنیم. در هر مورد دامنه ها مقادیری از \(x\) هستند که در آنها فرمول معنادار باشد.

پاسخ فرمول \(y=x^2\) یک مقدار حقیقی \(y\) به ازاء هر مقدار حقیقی \(x\) می دهد، بنابراین دامنۀ آن \((-\infty,\infty)\) می باشد. بُرد \(y=x^2\) برابر با \([0,\infty)\) است زیرا مربع هر عدد حقیقی، عددی غیرمنفی می باشد و هر عدد غیرمنفی \(y\) مربعِ ریشۀ دوم (جذر) خودش می باشد، \(y=\biggl( \sqrt{y} \biggr)^2\) برای \(y \ge 0\) .
فرمول \(y=\frac{1}{x}\) به ازاء هر مقدار \(x\) به جز \(x=0\)، یک مقدار \(y\) حقیقی می دهد. برای پابرجایی قوانین علم حساب (arithmetic)، ما نمی توانیم عددی را بر صفر تقسیم کنیم. بُرد \(y=\frac{1}{x}\)، مجموعۀ کسرهای متقابل (reciprocals) تمامی اعداد حقیقی غیر صفر، برابر با مجموعۀ تمامی اعداد حقیقی غیر صفر می باشد، از اینرو \(y=\frac{1}{\frac{1}{y}}\). به این معنا که، برای \(y \ne 0\)، عدد \(x=\frac{1}{y}\)، مقدار ورودی اختصاص داده شده به مقدار خروجی \(y\) می باشد.
فرمول \(y=\sqrt{x}\) تنها در صورتی یک مقدار حقیقی \(y\) می دهد که \(x \ge 0\) باشد. برد \(y=\sqrt{x}\) برابر با \([0,\infty)\) است زیرا هر عدد غیر منفی، جذر عددی می باشد (یعنی، جذرِ جذر خودش می باشد).
در \(y=\sqrt{4-x}\)، مقدار \(4-x\) نمی تواند منفی باشد. بدین معنا که، \(4-x \ge 0\) یا \(x \le 4\). این فرمول به ازاء تمام مقادیر \(x \le 4\)، عدد حقیقی می دهد. برد \(\sqrt{4-x}\) برابر با \([0,\infty)\) ،مجموعۀ تمام اعداد غیرمنفی، می باشد.
فرمول \(y=\sqrt{1-x^2}\) به ازاء هر \(x\) در بازۀ بستۀ \(-1\) تا \(1\) یک مقدار حقیقی تولید می کند. خارج از این دامنه، \(1-x^2\) منفی است و جذر آن عددی حقیقی نمی باشد. مقادیر \(1-x^2\) از \(0\) تا \(1\) در دامنۀ داده شده تغییر می کنند، و جذر این مقادیر نیز چنین هستند. برد \(\sqrt{1-x^2}\) برابر با \([0,1]\) می باشد.

1.1 توابع و نمودارهای آنها (Functions and Their Graphs)
توابع ابزاری برای توصیف دنیای واقعی به لحاظ ریاضی می باشند. یک تابع می تواند با یک معادله (equation)، یک نمودار (graph)، یک جدول عددی (numerical table)، یا یک توصیف کلامی (verbal description) نمایش داده شود؛ ما در طول این کتاب از هر چهار نوع نمایش توابع استفاده خواهیم کرد. این بخش این مفاهیم توابع را مورد بررسی قرار می دهد.
توابع؛ دامنه و بُرد (Functions; Domain and Range)
دمایی که آب در آن به جوش می آید به ارتفاع از سطح دریا بستگی دارد (هرچقدر بالاتر بروید نقطۀ جوش سقوط می کند). بهرۀ پرداختی برای پول نقد سرمایه گذاری شده به طول مدتی که آن سرمایه نگهداشته شده است بستگی دارد. مساحت یک دایره به شعاع آن بستگی دارد. مسافت پیموده شده توسط یک شیء با سرعت ثابت در امتداد یک مسیر خط مستقیم، به زمان سپری شده بستگی دارد.
در هر مورد، مقدار کمیت یک متغیر، فرض کنید \(y\)، به مقدار کمیت متغیر دیگری بستگی دارد، که ممکن است آن را \(x\) بنامیم. ما می گوییم که \(y\) تابعی از \(x\) است (y is a function of x) و این را به صورت نمادین اینگونه می نویسیم:
$$y=f(x)$$
این را اینگونه می خوانیم: \(y\) برابر است با افِ ایکس (y equals ƒ of x)
در این نشانه گذاری، نماد \(f\) نشان دهندۀ تابع است، حرف \(x\) متغیر مستقل (independent variable) است که مقدار ورودی \(f\) را نشان می دهد، و \(y\) متغیر وابسته (dependent variable) یا مقدار خروجی \(f\) در \(x\) می باشد.
تعریف: یک تابع \(f\) از یک مجموعۀ \(D\) به یک مجموعۀ \(Y\) یک قاعده است که یک عنصر یکتا (unique)، \(f(x) \in Y\) را به هر عنصر \(x \in D\) اختصاص می دهد.
مجموعۀ \(D\) متشکل از تمامی مقادیر ورودی (input values) ممکن، دامنۀ (domain) این تابع نامیده می شود. مجموعۀ تمامی مقادیر خروجی (output values) از \(f(x)\) همینطور که \(x\) در سراسر \(D\) تغییر می کند، بُرد (range) این تابع نامیده می شود. این بُرد ممکن است شامل تمامی عناصر موجود در مجموعۀ \(Y\) نشود. دامنه و برد یک تابع می تواند هر مجموعه ای از اشیاء باشد، اما اغلب در حسابان آنها مجموعه ای از اعداد حقیقی (real numbers) می باشند که به نقاطی از یک خط مختصات تفسیر می گردند. (در فصل های \(\text{13-16}\)، با توابعی مواجه خواهیم شد که در آنها عناصر این مجموعه ها نقاطی در صفحۀ مختصات یا در فضا می باشند.)
اغلب یک تابع با یک فرمول معین می شود که چگونگی محاسبۀ مقدار خروجی از روی متغیر ورودی را توصیف می کند. به عنوان مثال، معادلۀ \(A=\pi r^2\) یک قاعده است که مساحت \(A\) یک دایره را از روی شعاع آن \(r\) محاسبه می کند (بنابراین، \(r\)، که به عنوان یک طول تفسیر می شود، در این فرمول فقط می تواند مثبت باشد). هنگامیکه یک تابع \(y=f(x)\) را با یک فرمول تعریف می کنیم و دامنۀ آن به صراحت بیان نمی شود یا با مفاد آن محدود نمی گردد، این دامنه به شکل بزرگترین مجموعه از مقادیر حقیقی \(x\) در نظر گرفته می شود که برای آنها این فرمول یک مقدار حقیقی \(y\) را نتیجه می دهد، به این دامنه، دامنۀ طبیعی (natural domain) گفته می شود. اگر می خواهیم این دامنه را به نحوی محدود کنیم، باید چنین بگوییم. دامنۀ \(y=x^2\) کل مجموعۀ اعداد حقیقی می باشد. فرض کنید می خواهیم دامنۀ این تابع را به مقادیر مثبت \(x\) محدود کنیم، آن را اینگونه می نویسیم:
$$y=x^2, x \gt 0$$
تغییر دادن دامنه ای که بر روی یک فرمول اِعمال می شود، معمولاً برد آن را نیز تغییر می دهد. بُرد \(y=x^2\) برابر با \([0,\infty)\) می باشد. برد \(y=x^2, x \ge 2\) برابر با مجموعۀ تمامی اعداد بدست آمده از مربع ساختن اعداد بزرگتر یا مساوی \(2\) می باشد. در نشانه گذاری مجموعه ها این برد به یکی از سه شکل زیر نوشته می شود:
$$\{x^2| x \ge 2\} \text{ or } \{ y|y \ge 4 \} \text{ or } [4,\infty)$$
هنگامیکه برد یک تابع مجموعه ای از اعداد حقیقی باشد، گفته می شود که آن تابع با مقدار حقیقی (real-valued) می باشد. دامنه ها و بردهای بیشتر توابع حقیقی (real-valued functions) از یک متغیر حقیقی که در نظر می گیریم، بازه ها (intervals) یا ترکیبی از بازه ها می باشند. بازه ها می توانند باز (open)، بسته (closed)، یا نیمه باز (half open) باشند، و می توانند متناهی (finite) یا نامتناهی (infinite) باشند. گاهی اوقات یافتن برد یک تابع آسان نمی باشد.
یک تابع \(f\) مانند دستگاهی است که هرگاه که یک مقدار ورودی \(x\) را از دامنه اش به آن وارد می کنیم یک مقدار خروجی \(f(x)\) را در بُردش تولید می کند (شکل \(\text{1.1}\)). دکمه های توابع بر روی یک ماشین حساب مثالی از یک تابع در شکل یک دستگاه می باشد. به عنوان مثال، دکمۀ \(\sqrt{x}\) بر روی یک ماشین حساب، هرگاه که شما یک عدد غیرمنفی را وارد کنید و این دکمه را بفشارید، یک مقدار خروجی (جذر) به شما می دهد.

همچنین یک تابع می تواند به شکل یک نمودار فلش (arrow diagram) در نظر گرفته شود (شکل \(\text{1.2}\)). هر فلش یک عنصر از دامنۀ \(D\) را با یک عنصر یکتا یا واحد در مجموعۀ \(Y\) مرتبط می سازد. در شکل \(\text{1.2}\) فلش ها نشان می دهند که \(f(a)\) به \(a\) مرتبط است، \(f(x)\) به \(x\) مرتبط است، و به همین ترتیب. توجه داشته باشید که یک تابع می تواند به ازاء دو مقدار ورودی متفاوت از دامنۀ آن مقدار یکسانی را داشته باشد (همچنانکه در \(f(a)\) از شکل \(\text{1.2}\) رخ داده است)، اما هر عنصر ورودی \(x\) با یک مقدار خروجی واحد از \(f(x)\) مرتبط است.

مثال 1 بیایید دامنۀ طبیعی و بردهای مرتبط با آن را برای چند تابع ساده بررسی کنیم. در هر مورد دامنه ها مقادیری از \(x\) هستند که در آنها فرمول معنادار باشد.

پاسخ فرمول \(y=x^2\) یک مقدار حقیقی \(y\) به ازاء هر مقدار حقیقی \(x\) می دهد، بنابراین دامنۀ آن \((-\infty,\infty)\) می باشد. بُرد \(y=x^2\) برابر با \([0,\infty)\) است زیرا مربع هر عدد حقیقی، عددی غیرمنفی می باشد و هر عدد غیرمنفی \(y\) مربعِ ریشۀ دوم (جذر) خودش می باشد، \(y=\biggl( \sqrt{y} \biggr)^2\) برای \(y \ge 0\) .
فرمول \(y=\frac{1}{x}\) به ازاء هر مقدار \(x\) به جز \(x=0\)، یک مقدار \(y\) حقیقی می دهد. برای پابرجایی قوانین علم حساب (arithmetic)، ما نمی توانیم عددی را بر صفر تقسیم کنیم. بُرد \(y=\frac{1}{x}\)، مجموعۀ کسرهای متقابل (reciprocals) تمامی اعداد حقیقی غیر صفر، برابر با مجموعۀ تمامی اعداد حقیقی غیر صفر می باشد، از اینرو \(y=\frac{1}{\frac{1}{y}}\). به این معنا که، برای \(y \ne 0\)، عدد \(x=\frac{1}{y}\)، مقدار ورودی اختصاص داده شده به مقدار خروجی \(y\) می باشد.
فرمول \(y=\sqrt{x}\) تنها در صورتی یک مقدار حقیقی \(y\) می دهد که \(x \ge 0\) باشد. برد \(y=\sqrt{x}\) برابر با \([0,\infty)\) است زیرا هر عدد غیر منفی، جذر عددی می باشد (یعنی، جذرِ جذر خودش می باشد).
در \(y=\sqrt{4-x}\)، مقدار \(4-x\) نمی تواند منفی باشد. بدین معنا که، \(4-x \ge 0\) یا \(x \le 4\). این فرمول به ازاء تمام مقادیر \(x \le 4\)، عدد حقیقی می دهد. برد \(\sqrt{4-x}\) برابر با \([0,\infty)\) ،مجموعۀ تمام اعداد غیرمنفی، می باشد.
فرمول \(y=\sqrt{1-x^2}\) به ازاء هر \(x\) در بازۀ بستۀ \(-1\) تا \(1\) یک مقدار حقیقی تولید می کند. خارج از این دامنه، \(1-x^2\) منفی است و جذر آن عددی حقیقی نمی باشد. مقادیر \(1-x^2\) از \(0\) تا \(1\) در دامنۀ داده شده تغییر می کنند، و جذر این مقادیر نیز چنین هستند. برد \(\sqrt{1-x^2}\) برابر با \([0,1]\) می باشد.
لیست دوره های آموزش ریاضی در سایت خوش آموز
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.
- دوره آموزشی رایگان ریاضی پایه و پیش جبر
- تمرینات دوره آموزشی ریاضی پایه و پیش جبر
- دوره آموزشی رایگان جبر 1
- دوره آموزشی رایگان جبر 2
- دوره آموزشی رایگان هندسه
- دوره آموزشی رایگان مثلثات
- دوره آموزشی رایگان پیش حسابان 1
- دوره آموزشی رایگان حسابان 1
- آموزش رایگان حسابان پیشرفته
برای مشاهدۀ همۀ دوره های ریاضی اینجا کلیک کنید.





نمایش دیدگاه ها (0 دیدگاه)
دیدگاه خود را ثبت کنید: